Zur Analyse von erster und zweiter Welle wurde eine Gaußsche Glockenfunktion verwendet, um den Verlauf der täglichen Zahl an Neuinfektionen zu beschreiben. Dabei wird ein symmetrischer Verlauf von einem asymmetrischen Verlauf unterschieden (siehe hierzu auch Abschnitt „1. Welle“). Auf dieser Seite wird nur der Verlauf der Daten beschrieben. Weitere Auswertungen und Prognosen folgen.
Die symmetrische Funktion hat die Form:
gs(x) = A * (1/(sqrt(2 * pi) * \sigma)) * e^{(-0.5 * ((x-\mu)/\sigma)^{2})} + CBei der asymmetrische Funktion wächst \sigma mit zunehmender Zeit um den Wert (x-\mu)*asym. Je größer asym, umso stärker ist der asymmetrische Effekt. Daraus resultiert die Form:
g(x) = A * (1/(sqrt(2 * pi) * \sigma)) * e^{(-0.5 * ((x-\mu)/((\sigma+(x-\mu)*asym)))^{2})} + CDie Zahl an täglichen Neuinfektionen wurde dabei über ein gleitendes 7-Tage Mittel geglättet, wobei sich der Wert zu Tag t_{n} aus (t_{n-3} + \dots + t_{n+3})/7 berechnet.
1. Welle
Zunächst wird die erste Welle betrachtet, da diese bereits vollständig durchlaufen ist und somit eine bessere Datenbasis liefert. Bei der Analyse der ersten Welle fällt auf, dass die originale Gauß-Funktion den Verlauf der realen Daten nur bedingt beschreiben kann, da diese symmetrisch um das Maximum verläuft. Die reale Welle hingegen steigt steiler an und fällt etwas flacher ab. Die Kurve verläuft somit asymmetrisch zum Maximum. Die Gauß-Funktion wurde daher um einen „Asymmetrie-Faktor“ erweitert. Das Ergebnis ist in der folgenden Abbildung gezeigt. Die realen Daten sind als schwarze Kreuze dargestellt, die originale Gauß-Funktion als gestrichelte, rote Linie, die asymmetrische Kurve als durchgezogene, rote Linie. Die grauen, horizontalen Linien schneiden die jeweiligen Glockenkurven in der Mitte.
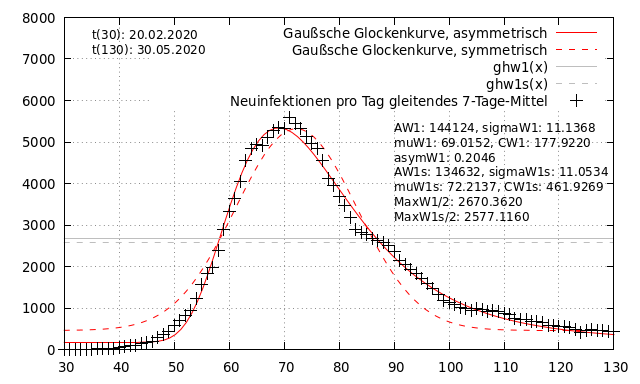
Die asymmetrische Kurve beschreibt den Verlauf der realen Daten in allen Bereichen besser als die symmetrische Kurve. Das Maximum der symmetrischen Kurve berechnet sich zu 5.144, dass der asymmetrischen Kurve zu 5.340 Neuinfektionen pro Tag. Der Zeitpunkt des symmetrischen Maximums berechnet sich zu t_{72}, der des asymmetrischen zu t_{69}. Das heißt, das Maximum der asymmetrischen Kurve ist etwa 4% größer und wird 3 Tage früher erreicht. Die Breite der Glocke wird durch \sigma beschrieben und berechnet sich zu 11. Der Asymmetriefaktor wird zu 0,2 berechnet. Letzterer bedeutet, das \sigma mit Fortschreiten der Welle deutlich größer werden muss, um den Verlauf noch treffend beschreiben zu können. Ein Wert von 0,2 für den Asymmetriefaktor bedeutet, dass \sigma um 1 oder 9% pro 5 Tage wächst.
2. Welle – Entwicklung über die Zeit – symmetrisch
Da die zweite Welle gerade ihr Maximum erreicht hat, ist die Datenbasis für eine Approximation einer Kurvenfunktion an die Daten mit größeren Fehlern behaftet, als wenn die Daten vollständig vorhanden sind, wie dies für die erste Welle der Fall ist. Dies gilt im Besonderen für eine Approximation über eine asymmetrische Kurve, da sich die fallende Flanke von der steigenden unterscheidet im Gegensatz zur symmetrischen. Es ist daher damit zu rechnen, dass sich die ermittelten Werte Tag für Tag etwas ändern. In diesem Abschnitt wird zunächst nur eine Approximation über eine symmetrische Gauß-Funktion betrachtet.
Die folgende Abbildung zeigt dazu einen Vergleich einer Approximation mit einer Gauß-Funktion zu t_{296} (12.11.2020), durchgezogene, rote Linie zu einer Approximation der gleichen Gauß-Funktion zu t_{301} (17.11.2020).
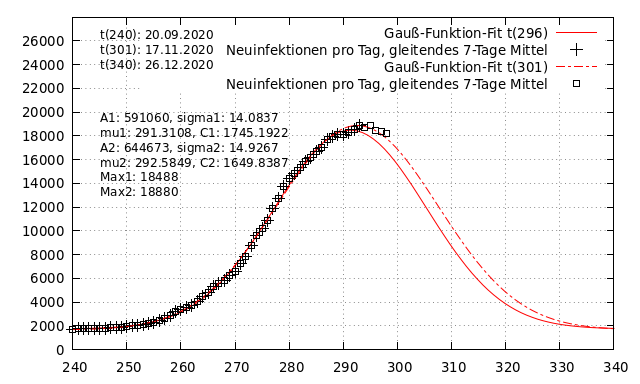
| t_{296} | t_{301} | |
| Maximum | 18.488 | 18.880 |
| Tag(Max) | 291,3 | 292,6 |
| \sigma | 14,1 | 14,9 |
Das für t_{301} berechnete Maximum ist damit um circa 2% größer und wird 1,3 Tage später erreicht. \sigma ist um 5% größer.
2. Welle – Entwicklung über die Zeit – asymmetrisch
Als nächstes werden derselbe Zeitbereich betrachtet, wie im vorherigen Abschnitt. Dieses mal wird aber eine asymmetrische „Gauß-Funktion“ zur Approximation verwendet. Einmal an die Daten, die bis zu t_{296} vorlagen, ein zweites Mal an die Daten, die bis zu t_{301} vorlagen.
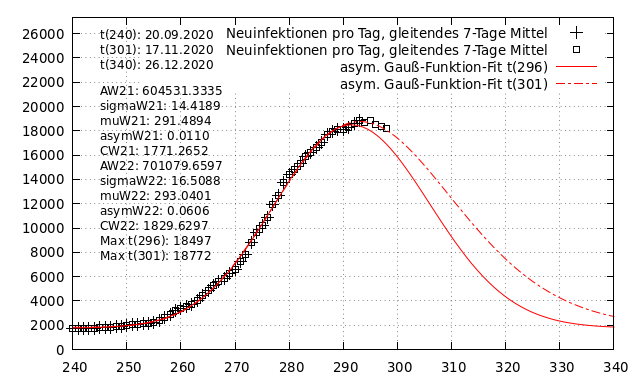
Es berechnen sich folgende Werte:
| t_{296} | t_{301} | |
| Maximum | 18.497 | 18.772 |
| Tag(Max) | 291,5 | 293 |
| \sigma | 14,4 | 16,5 |
| asym | 0,01 | 0,06 |
Das für t_{301} berechnete Maximum ist damit um circa 1,5% größer und wird 1,5 Tage später erreicht. \sigma ist um 13% größer, der Asymmetrie-Faktor um Faktor 6. Im Vergleich zur ersten Welle ist \sigma um 24% bzw. 33% größer, die 2. Welle ist also breiter, die Asymmetrie ist aber – noch – deutlich kleiner. Es wird interessant sein, die weitere Entwicklung von \sigma und im Besonderen die des Asymmetrie-Faktors zu beobachten.
Ausblick
Die gewonnen Erkenntnisse, wie der Verlauf der Wellen über eine asymmetrische Gauß-Funktion beschrieben werden kann, wird in folgenden Beiträgen genutzt, um die weitere Entwicklung zu prognostizieren und den Effekt des Lockdowns zu bewerten.