Zur Analyse von erster und zweiter Welle wurde eine Gaußsche Glockenfunktion verwendet, um den Verlauf des gleitenden Mittels über die tägliche Zahl an Neuinfektionen zu beschreiben. Eine rein phänomenologische Betrachtung der Welle im Frühjahr zeigte, dass diese nicht symmetrisch um das Maximum verlief sondern dass der Anstieg schneller erfolgte als der Abfall. Es war möglich, die erste Welle mit einer Gauß’schen Glockenfunktion zu beschreiben. Die Breite dieser Glockenfunktion wird durch einen Parameter bestimmt, der sigma (\sigma) genannt wird. Je größer sigma, desto breiter die Glocke. In einem ersten Ansatz wurde die Asymmetrie durch ein über die Zeit größer werdendes \sigma abgebildet. (Details siehe hier).
Bei der Untersuchung von Häufigkeitsverteilungen fand man heraus, dass die Gauß-Funktion eine bessere Betrachtung der Binomialverteilung ermöglicht. Es hat sich des Weiteren gezeigt, dass viele in der Praxis auftretende Häufigkeitsverteilungen glockenförmig sind. Die Gauß-Funktion enthält einen Wahrscheinlichkeitswert für das Ergebnis einer einzelnen Aktion. So ist zum Beispiel die Wahrscheinlichkeit p=0,5, dass beim Wurf einer idealen Münze „Kopf“ fällt.
Die Gauß-Funktion für eine Binomialverteilung hat die Form:
g(x) = \frac{1}{\sigma * \sqrt{2 * pi}} * e^{-p * (\frac{x-\mu}{\sigma})^{2}}
Die folgende Abbildung zeigt den Verlauf der Glockenkurve für \sigma=10 und \mu=0 für die Wahrscheinlichkeiten p: 0,2; 0,4; 0,6\text{ und }0,8.
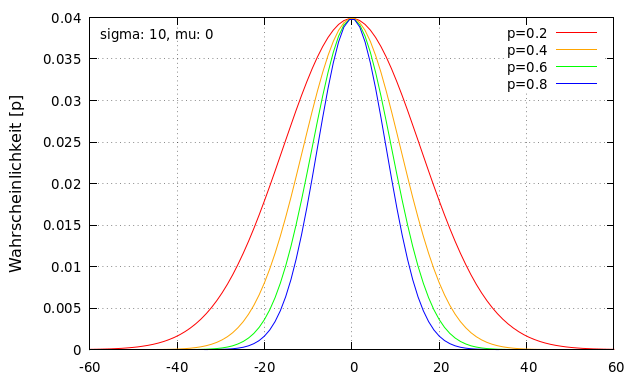
Aus der Darstellung ist ersichtlich, dass die Glockenfunktion mit kleiner werdendem p breiter wird.
Übertragung auf Corona
Aus theoretischen Überlegungen (Grenzwertsatz) kann abgeleitet werden, dass viele Häufigkeitsverteilungen glockenförmig sind. Dieser Ansatz soll nun auf die Entwicklung der Zahl täglicher Neuinfektionen übertragen werden. Diese Übertragung ist durchaus kritisch zu betrachten: Die verwendete „Glockenfunktion“ ist modifiziert und nicht symmetrisch um einen Mittelwert. Die verwendete Stichprobe (für Tests ausgewählte Personen) ist nicht zufällig, da die Personen nach Vorgaben des RKI nach bestimmten Kriterien ausgewählt werden. Dennoch wird hier der Versuch einer Übertragung vorgenommen. Vom Grippevirus, wie auch für andere Rhinoviren, die Erkältungskrankheiten auslösen, ist bekannt, dass Menschen häufiger in der kalten als in der warmen Jahreszeit erkranken. Daraus lässt sich ableiten, dass die Wahrscheinlichkeit, an einem solchen Virus zu erkranken, über die Zeit Schwankungen unterliegt. Lässt man p aus der obigen Gleichung g(x) in Form eines Sinus größer und kleiner werden, soll dies die Schwankungen über die Zeit simulieren. Da die Glocke über p in der Breite verändert werden kann, sollte es möglich sein, über ein sich veränderndes p die fallende Flanke langsamer abfallen zu lassen als die ansteigende zunimmt. Eine Glockenfunktion kann dabei nur genau eine Welle beschreiben und keine zwei aufeinanderfolgenden. Für jede Welle muss daher eine eigene Funktion definiert werden.
1. Welle
Zunächst wird die erste Welle betrachtet, da diese bereits vollständig durchlaufen ist und somit eine bessere Datenbasis liefert. Eine Ausnahme stellt die Zahl der Infizierten vor der ersten Welle dar. Für diese Zeit sind keine Daten vorhanden. Auf Grund der Neuartigkeit des Virus kann angenommen werden, dass die Zahl der täglichen Neuinfektionen tatsächlich bei null lag. Dies darf als Ausnahmefall betrachtet werden. Seit Beginn des Jahres ist das Virus in unserer Gesellschaft vorhanden. Es soll nun untersucht werden, inwiefern eine Gauß-Funktion, deren Wahrscheinlichkeit p um einen Mittelwert schwankt, in der Lage ist, den asymmetrischen Verlauf der ersten Welle zu beschreiben. Diese Funktion hat folgende Form:
gp(x) = A * \frac{1}{\sigma * \sqrt{2 * pi}} * e^{-(p + a * sin(\frac{2}{b} * (x+c))) * (\frac{x-\mu}{\sigma})^{2}}
Diese Gauß-Funktion unterscheidet sich von der weiter oben gezeigten darin, dass p um einen Mittelwert schwankt. Die Amplitude der Schwankung wird durch den Parameter klein a angegeben. Parameter b entspricht der Periodendauer des Sinus in Tagen. Parameter c gibt die Phasenverschiebung in Tagen an. Parameter groß A wird verwendet, um die Kurve an die Zahl der täglichen Neuinfektionen pro 100.000 und Woche anzupassen.
Die folgende Abbildung zeigt den über ein 7-Tage-Mittel geglätteten Verlauf der Zahl täglicher Neuinfektionen normiert auf die relative Testhäufigkeit als schwarze Linie. Die rote, durchgezogene Linie zeigt die asymmetrische Gauß-Funktion als Approximation an die realen Daten. Die rote, gestrichelte Linie zeigt die symmetrische Gaußfunktion (konstantes p. Die graue Linie zeigt den Sinus um den Faktor 500 skaliert, zur besseren Veranschaulichung. Die im Weiteren angegebenen Werte ergeben sich aus der Approximation der modifizierten Gauß-Funktion an die realen Daten. Die Wahrscheinlichkeit p, sich mit dem Virus zu infizieren, schwankt zwischen 0,05 und 0,2 (oder 5% und 20%). Das Maximum des Sinus liegt an t_{27} (17.02.2020) und nimmt bis zum Ende der ersten Welle kontinuierlich ab. Die Periodendauer des Sinus beträgt 190 Tage. Das Maximum der asymmetrischen Glockenkurve wird an t_{70} (31.03.2020) erreicht und beträgt 187 Neuinfektionen pro hunderttausend und Woche. Das Maximum liegt 43 Tage nach dem letzten Maximum von p. Die Breite der Glockenkurve beträgt, gemessen als \sigma, 6,55. Zusammenfassend kann man feststellen, dass die über eine sich ändernde Wahrscheinlichkeit modifizierte Gauß-Funktion den Verlauf der realen Infektionszahlen sehr gut beschreibt. Es kann damit gezeigt werden, dass eine sich ändernde Wahrscheinlichkeit ausreicht, den asymmetrischen Kurvenverlauf zu beschreiben.
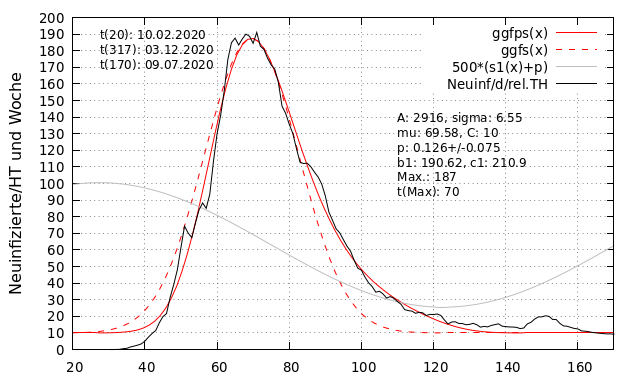
2. Welle
Die zweite Welle hat ihr Maximum nach Datenlage an t_{317} (03.12.2020) und Berechnungsart an t_{307} (23.11.2020) erreicht. Dies liegt 10 Tage vor dem gezeigten Auswertezeitpunkt. Die Datenbasis für die Approximation einer Kurvenfunktion an die zweite Welle ist mit größeren Fehlern behaftet, da die Daten für die zweite Welle noch nicht vollständig vorhanden sind, wie dies für die erste Welle der Fall ist. Dies gilt im Besonderen für eine Approximation über eine asymmetrische Kurve, da sich die fallende Flanke von der steigenden im Gegensatz zur symmetrischen unterscheidet. Es ist daher damit zu rechnen, dass sich die ermittelten Werte Tag für Tag etwas ändern.
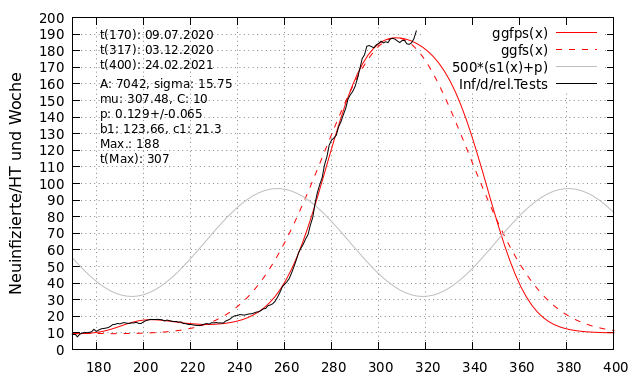
Die folgende Abbildung zeigt, ebenso wie zur ersten Welle, den über ein 7-Tage-Mittel geglätteten Verlauf der Zahl täglicher Neuinfektionen normiert auf die relative Testhäufigkeit als schwarze Linie. Die rote, durchgezogene Linie zeigt die asymmetrische Gauß-Funktion. Die rote, gestrichelte Linie zeigt die symmetrische Gaußfunktion (konstantes p). Die graue Linie zeigt den Sinus um den Faktor 500 skaliert, zur besseren Veranschaulichung. Die Wahrscheinlichkeit p schwankt zwischen 0,064 und 0,194 (oder 6,4% und 19,4%) und ist nahezu gleich der Wahrscheinlichkeit, die für die erste Welle über die Approximation ermittelt wurde. Das letzte Maximum der Sinusfunktion vor dem Maximum der zweiten Welle liegt an t_{257} (04.10.2020), nimmt bis etwas nach dem Maximum ab, um danach wieder anzusteigen. Die Periodendauer beträgt 123,7 Tage und ist damit deutlich kürzer als zur ersten Welle berechnet. Das Maximum der Glockenkurve errechnet sich zu t_{307} (23.11.2020) und beträgt 188 Neuinfektionen pro hunderttausend und Woche. Dies entspricht fast genau dem Wert der ersten Welle von 187 Neuinfektionen pro hunderttausend und Woche. Das Maximum liegt 50 Tage nach dem letzten Maximum von p. Die Breite der Glockenkurve beträgt \sigma = 15,75. Die zweite Welle ist damit gut doppelt so breit, d.h. dauert doppelt so lange, wie die erste Welle.
Sehr auffallend ist, dass die Approximation selbst den ersten kleinen Anstieg zwischen etwa t_{180}\text{ und }t_{240} nahezu perfekt beschreibt.
| 1. Welle | 2. Welle | |
| Max. Neuinf/HT und Woche | 187 | 188 |
| \sigma | 6,55 | 15,75 |
| p | 0,126\pm0,075 | 0,129\pm0,065 |
| Periodendauer Sinus [d] | 191 | 124 |
Zusammenfassung
- Es konnte gezeigt werden, dass die erste und bereits vollständig durchlaufene Welle durch eine Gauß-Funktion beschrieben werden kann, deren Wahrscheinlichkeit für das Eintreten eines Ereignisses (infiziert) sinusförmig schwankt
- Die Wahrscheinlichkeit für das Eintreten eines Ereignisses (sich zu infizieren) ist in beiden Wellen nahezu gleich
- Die zweite Welle ist gut doppelt so breit, wie die erste
- Die Glockenkurve ist nicht symmetrisch. Dadurch stellt sich die Frage, wie die einzelnen Parameter interpretiert und welche Schlüsse gezogen werden dürfen
- Für das Einzelereignis ist nicht klar, inwiefern damit gemeint ist, mit dem Virus infiziert zu sein oder daran zu erkranken. Aktuell kann nur festgehalten werden, dass es dem Ergebnis des PCR Tests entspricht
- Die Gruppe der für Tests ausgewählte Personen stellt keine Stichprobe im Sinne der Wahrscheinlichkeitsrechnung dar, da die zu testenden Personen nach vom RKI vorgegebenen Kriterien ausgewählt werden
- Das vielleicht überraschendste Ergebnis ist, dass die modifizierte Glockenkurve den ersten kleinen Anstieg vor der eigentlichen Welle abbilden kann
Die gewonnen Erkenntnisse, dass und wie der Verlauf der Wellen über eine asymmetrische Gauß-Funktion beschrieben werden kann, wird in folgenden Beiträgen vor allem dazu genutzt, die weitere Entwicklung der prognostizierten Breite der Glockenkurve (\sigma) zu beobachten. Damit sollte es möglich sein, die Abklingphase und das Ende der zweiten Welle zu prognostizieren. Es sollte auch möglich sein, den Effekt des Lockdowns bewerten zu können.