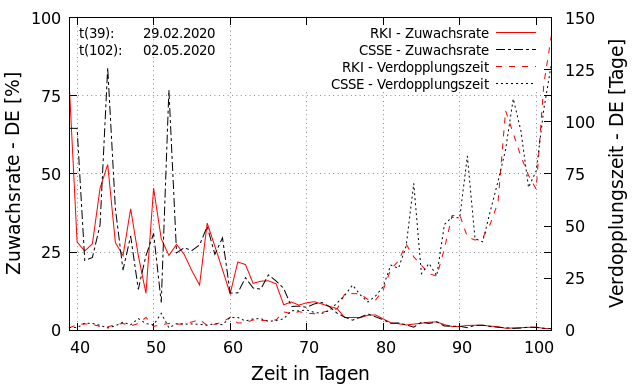
Die Abbildung zeigt die Entwicklung der Zuwachsrate in Prozent (linke Y-Achse), also die relative Zunahme an Infizierten im Vergleich zum Vortag sowie die Entwicklung der Verdopplungszeit in Tagen (rechte Y-Achse) seit dem 29.02.2020.
Man erkennt deutlich, dass die Zuwachsrate im dargestellten Zeitraum deutlich und stetig ab- und die Verdopplungszeit entsprechend zunimmt.
Die Verdopplungszeit ist seit dem 28.03.2020 größer als 6 Tage und seit dem 03.04.2020 größer als 9 Tage. Mit Stand vom 13.04.2020 liegt die Verdopplungszeit nun bei über 40 Tagen. Seit vier Tagen nimmt die Verdopplungszeit steil zu, von 14 auf 41 Tage. Das sind 27 Tage plus in 4 Tagen oder ein Plus von 7 Tagen Verdopplungszeit pro Kalendertag!
Ostern
Mit den Daten zum 14.04.2020, also unmittelbar nach dem Osterwochenende fällt die Verdopplungszeit nach den RKI Daten von 41 auf 35 Tage. Ich habe die Daten der John Hopkins Universität (CSSE) in der Abbildung ergänzt. Grundsätzlich verlaufen die Kurven parallel, nur dass zum 14.04.2020 sich 70 Tage (nach CSSE) und nicht 35 Tage (RKI) als Verdopplungszeit ergeben. Man wird die nächsten Tage abwarten müssen, wie fehlerbehaftet die Zahlen vom Osterwochenende waren.
Nach Ostern ist die Verdopplungszeit in der Tat deutlich gefallen, von 70 auf 27 Tage für die CSSE Daten und von 35 auf 31 für die RKI Daten. Ich gehe aber davon aus, dass die Werte für die Verdopplungszeit bis zum kommenden Wochenende wieder ansteigen.
Nach Ostern
Freitag nach Ostern: Der Wert der Verdopplungsrate, der für die CSSE Daten nach Ostern so dramatisch von 70 auf 27 Tage abstürzte, steigt nun wieder. Am 17.04.2020 betrug der Wert 32 Tage. Der Wert für die RKI Daten fällt weiter auf nunmehr 27 Tage.
Sonntag nach Ostern: Die Werte der Verdopplungszeit steigen wieder! Nach RKI und CSSE liegt die Verdopplungszeit wieder bei 54 Tagen.
Die Verdopplungszeit nimmt in Schwingungen weiterhin kontinuierlich zu und liegt Anfang Mai bei über 100 Tagen.
Planung von Maßnahmen durch Regierung
Das Innenministerium hatte schärfere Maßnahmen verlangt, um die Verdopplungszeit schneller zu vergrößern, so dass eine Verdopplungszeit von 9 Tagen nicht erst Ende sondern Mitte April erreicht wird. Nun ist dieses Ziel auch ohne weitere Verschärfung der Maßnahmen nicht nur erreicht sondern deutlich – Faktor 3 – überschritten.
Was nun, Herr Minister? Bleibt es bei der Ankündigung „die allgemeinen Ausgangsbeschränkungen ab 20. April schrittweise“ zu lockern? Verfolgt man die Äußerungen der Ministerpräsidenten am Osterwochenende, dann könnte man das meinen.
Seit Anfang Mai liegt der Wert der Verdopplungsrate bei über 100 Tagen. Das ist mehr als das zehnfache, das man sich Ende März als Ziel gesetzt hat. Trotzdem werden Lockerungen nur zögerlich umgesetzt. Es entsteht der Eindruck, dass die Exekutive nicht so genau weiß, auf welchen Wert – Verdopplungszeit, Reproduktionsrate (R) – man bei der Entscheidungsfindung fokussieren sollte. Dies führt nicht zu Transparenz gegenüber der Bevölkerung. Es stellt sich daher die Frage, ob die Regierung einfach nur schlecht beraten ist, ob sie bewusst die Lockerungen eher verzögern möchte oder ob sie einfach nur keinen Plan und damit keine Orientierung hat, die ihr einen transparenten Entscheidungsprozess ermöglicht.
Berechnung der Verdopplungszeit
An andere Stelle schrieb ich, dass bei sigmoidalem Verlauf einer Kurve, wie sie für die Zunahme der Zahl der Infizierten beobachtet werden kann, irgendwann ein Plateau erreicht wird. Erreichung eines Plateaus kann man dann so interpretieren, dass es irgendwann keine weitere Zunahme mehr gibt und man damit auch nicht mehr von einer Verdopplungszeit reden kann.
Jetzt zeigen die Auswertungen aber, dass der Wert, der für das Plateau Tag für Tag ermittelt wird langsam steigt. Man kann damit nicht von einem echten Plateau sprechen, zumindest nicht zum gegenwärtigen Zeitpunkt. Daher habe ich die Verdopplungszeit aus der Zuwachsrate ermittelt in der Form t = \frac{log_{2}}{log_{1+Zuwachsrate}}, wie in der obigen Abbildung gezeigt.